Question

Miguel is playing a game in which a box contains four chips with numbers written on them. Two of the chips have the number 1, one chip has the number 3, and the other chip has the number 5. Miguel must choose two chips, and if both chips have the same number, he wins $2. If the two chips he chooses have different numbers, he loses $1 (–$1).

Let X = the amount of money Miguel will receive or owe. Fill out the missing values in the table. (Hint: The total possible outcomes are six because there are four chips and you are choosing two of them.)

Answer 1

two = 1/6

and -1 = 5/6

Explanation:

Answer 2

`P(X_i=2) =(1)/(6)`

`P(X_i=-1) =(5)/(6)`

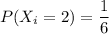
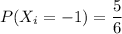
Explanation:

Given the numbers on the chips = 1, 1, 3 and 5

Miguel chooses two chips.

Condition of winning: Both the chips are same i.e. 1 and 1 are chosen.

Miguel gets $2 on winning and loses $1 on getting different numbers.

To find:

Probability of winning $2 and losing $1 respectively.

Solution:

Here, we are given 4 numbers 1, 1, 3 and 5 out of which 2 numbers are to be chosen.

This is a simple selection problem.

The total number of ways of selecting r numbers from n is given as:

`_nC_r = (n!)/(r!(n-r)!)`

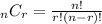
Here, n = 4 and r = 2.

So, total number of ways =
`_4C_2 = (4!)/(2!* 2!) = 6`

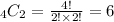
Total number of favorable cases in winning = choosing two 1's from two 1's i.e.
`_2C_2 = (2!)/(2! 0! ) = 1`

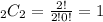
Now, let us have a look at the formula of probability of an event E:

`P(E) = \frac{\text{Number of favorable ways}}{\text{Total number of ways}}`

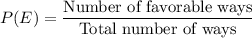
So, the probability of winning.

`P(X_i=2) =(1)/(6)`

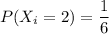
Total number of favorable cases for -1: (6-1) = 5

So, probability of getting -1:

`P(X_i=-1) =(5)/(6)`

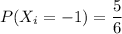
Please refer to the attached image for answer table.