Answer:
Area of polygon D = 10 square units
Explanation:
Given:
Polygon C has an area of 40 square units.
It is scaled with a scale factor of
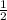 to form a new polygon D.
to form a new polygon D.
To find:
The area of polygon D = ?
Solution:
When any polygon is scaled to half, then all the sides of new polygon are half of the original polygon.
And the area becomes one-fourth of the original polygon.
Let us consider this by taking examples:
- First of all, let us consider a right angled triangle with sides 6, 8 and 10 units.
Area of a right angled triangle is given by:
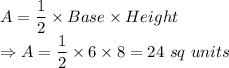
If scaled with a factor
 , the sides will be 3, 4 and 5.
, the sides will be 3, 4 and 5.
New area, A':
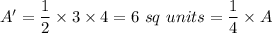
i.e. Area becomes one fourth.
- Let us consider a rectangle now.
Sides be 8 and 10 units.
Area of a rectangle, A =
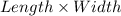 = 8
= 8
 10 = 80 sq units.
10 = 80 sq units.
Now after scaling, the sides will be 4 and 5 units.
New Area, A' = 4
 5 =20 sq units
5 =20 sq units
So,
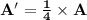
Now, we can apply the same in the given question.
 Area of polygon D =
Area of polygon D =
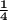
 Area of polygon C
Area of polygon C
Area of polygon D =
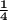
 40 = 10 sq units
40 = 10 sq units