Question

PLEASE HELP!!!!!Using the following image, solve for the trigonometry ratios of ∠D and ∠F.

Answer 1

x= 17

Next, find the trigonometry ratios of ∠D.

sin∠D= 8/17

cos∠D= 15/17

tan∠D= 8/15

Finally, find the trigonometry ratios of ∠F.

sin∠F=15/17

cos∠F= 8/17

tan∠F=15/8

Answer 2

By using the Pythagorean theorem, the value of x is 17. The trigonometry ratios of ∠D and ∠F include;

sin∠D = 8/17

cos∠D = 15/17

tan∠D = 8/15

sin∠F = 15/17

cos∠F = 8/17

tan∠F = 15/8

In Mathematics and Geometry, Pythagorean theorem is an Euclidean postulate that can be modeled or represented by the following mathematical equation:

`c^2=a^2+b^2`

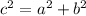
Where:

• a is the opposite side of a right-angled triangle.
• b is the adjacent side of a right-angled triangle.
• c is the hypotenuse of a right-angled triangle.

By applying Pythagorean's theorem to right-angled triangle DEF, the length of the hypotenuse (x) can be determined as follows;

`c^2=a^2+b^2\\\\x^(2) =8^2+15^2\\\\x^(2) =64+225\\\\x=√(289)`

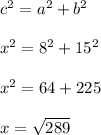
x = 17 units.

Next, we would determine the trigonometry ratios of angles D and F as follows;

sinθ = opposite side/hypotenuse

cosθ = adjacent side/hypotenuse

tanθ = opposite side/adjacent side

sin∠D = EF/DF

sin∠D = 8/17

cos∠D = DE/DF

cos∠D = 15/17

tan∠D = EF/DE

tan∠D = 8/15

sin∠F = DE/DF

sin∠F = 15/17

cos∠F = EF/DF

cos∠F = 8/17

tan∠F = DE/EF

tan∠F = 15/8

Information:

A clearer image of the right-angled triangle is shown below.