Question

Determine the polynomial equivalent to this expression.

x^2-9/x-3

A. x-3

B. -3x-9

C. x+3

D. x^2+3x​

Answer 1

`(x^2-9)/(x-3)= \Large \boxed{x+3}`

Explanation:

Hello,

We need to work a little bit of the expression to see if we can simplify.

Do you remember this formula?

for any a and b reals, we can write

`a^2-b^2=(a-b)(a+b)`

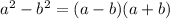
We will apply it.

For any x real number different from 3 (as dividing by 0 is not allowed)

`(x^2-9)/(x-3)=(x^2-3^2)/(x-3)=((x-3)(x+3))/(x-3)=x+3`

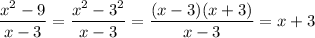
So the winner is C !!

Hope this helps.

Do not hesitate if you need further explanation.

Thank you