Question

The figure above shows a right-angled triangle OAB. AOC is a minor sector enclosed in the triangle. If OA = 7 cm, AB = 6 cm, calculate the area and perimeternof the shaded region.​ PLEASE HELP!

Answer 1

Explanation:

Given that:

OA = 7 cm, AB = 6 cm. ∠A = 90°, OA = OC = 7 cm

Using Pythagoras theorem: OB² = OA² + AB²

OB² = 6² + 7²=85

OB = √85 = 9.22 cm

to find ∠O, we use sine rule:

`(AB)/(sin(O))=(OB)/(sin(A))\\ \\sin(O)=(AB*sin(A))/(OB)=(6*sin(90))/(9.22) =0.65 \\\\O=sin^(-1)0.65=40.6^o`

AOC is a minor sector with radius 7 cm and angle 40.6

The Area of the triangle OAB = 1/2 × base × height = 1/2 × OA × AB = 1/2 × 7 × 6 = 21 cm²

Area of sector OAC =
`(\theta)/(360)*\pi r^2=(40.6)/(360)*\pi *7^2=17.37 \ cm^2`

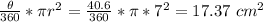
Area of shaded region = The Area of the triangle OAB - Area of sector OAC = 21 - 17.37 = 3.63 cm²

Perimeter of arc AC =
`(\theta)/(360)*2\pi r=(40.6)/(360)*2\pi *7=4.96\ cm`

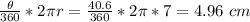
CB = OB - OC = 9.22 - 7 = 2.22

Perimeter of shaded region = AB + CB + arc AC = 6 + 2.22 + 4.96 = 13.18 cm