Answer:
Explanation:
Given that:
OA = 7 cm, AB = 6 cm. ∠A = 90°, OA = OC = 7 cm
Using Pythagoras theorem: OB² = OA² + AB²
OB² = 6² + 7²=85
OB = √85 = 9.22 cm
to find ∠O, we use sine rule:
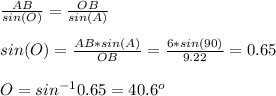
AOC is a minor sector with radius 7 cm and angle 40.6
The Area of the triangle OAB = 1/2 × base × height = 1/2 × OA × AB = 1/2 × 7 × 6 = 21 cm²
Area of sector OAC =
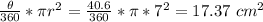
Area of shaded region = The Area of the triangle OAB - Area of sector OAC = 21 - 17.37 = 3.63 cm²
Perimeter of arc AC =
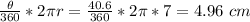
CB = OB - OC = 9.22 - 7 = 2.22
Perimeter of shaded region = AB + CB + arc AC = 6 + 2.22 + 4.96 = 13.18 cm