Question

The quadratic function f(x) = -x2 - 6x - 8 is graphed.

What are the solutions of the quadratic equation 0 =-
x2 - 6x-8?
2
O 2 and 4
-2 and 4
0-2 and -4
O2 and 4
2
X
-654-3
Next
Submit
Save and Exit
Mark this and return

Answer 1

The roots of the quadratic function
`f(x) = -x^(2)-6\cdot x -8` are
`x_(1) = -4` and
`x_(2) = -2`.

Explanation:

Let be
`f(x) = -x^(2)-6\cdot x -8`, the function is now graphed by using a graphing tool and whose outcome is added below as attachment. After looking the image, the roots of the polynomial are
`x_(1) = -4` and
`x_(2) = -2`, respectively. It can be also proved by algebraic means:

1)
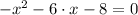`-x^(2)-6\cdot x -8=0` Given

2)
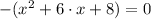`-(x^(2)+6\cdot x+8 )= 0` Distributive property/
`-(x) = -x`

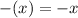
3)
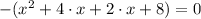`-(x^(2) +4\cdot x +2\cdot x +8)= 0` Addition

4)
`-[x\cdot (x+4)+2\cdot (x+4)] = 0` Distributive property/Associative property

5)
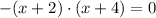`-(x+2)\cdot (x+4) = 0` Distributive property/Result

Which supports the graphic findings.

The roots of the quadratic function
`f(x) = -x^(2)-6\cdot x -8` are
`x_(1) = -4` and
`x_(2) = -2`.