Answer:
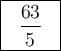
Explanation:
Hello,
"Find the sum of the following infinite geometric series"
infinite
We will have to find the limit of something when n tends to
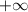
geometric series
This is a good clue, meaning that each term of the series follows a geometric sequence. Let's check that.
The sum is something like
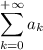
First of all, we need to find an expression for
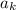
First term is
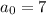
Second term is

Then
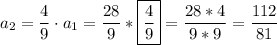
and...
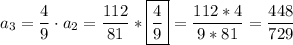
Ok we are good, we can express any term for k integer

So, for n positive integer
![\displaystyle \sum_(k=0)^(n) a_k=\displaystyle \sum_(k=0)^(n) 7\cdot ((4)/(9))^k=7\cdot (1-((4)/(9))^(n+1))/(1-(4)/(9))=(7*9*[1-((4)/(9))^(n+1)])/(9-4)=(63)/(5)\cdot [1-((4)/(9))^(n+1)}]](https://img.qammunity.org/2021/formulas/mathematics/college/27ytww2uqt993lzsbal38i8hi9c2879n30.png)
And the limit of that expression when n tends to
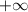 is
is
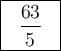
as
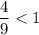
Hope this helps.
Do not hesitate if you need further explanation.
Thank you