Question

HELPPPImagine that as a ball is tossed, its motion is tracked on a coordinate plane. Given only a few of the points that the ball passes through, it is actually possible to determine the equation of the parabola that represents the ball’s path through the air. part a-Assume the ball passes through the points , , and . Use this data to set up a system of three equations and three unknowns (a, b, and c) that will allow you to find the equation of the parabola. Write the system in the space provided. part b-Use matrix manipulation to solve for a, b, and c. Set up a matrix equation for AX = B based on the system of equations you derived in part B where X is a matrix of the variables a, b, and c. Then, use Gauss-Jordan elimination to find the inverse of A. Finally, use your results to write the equation of the parabola. Show your work and final equation in the space provided. partc-Now that you have determined the equation of the parabola, assume that x represents the number of seconds that have passed since the ball was thrown and determine approximately how long it will take for the ball to hit the ground.

Answer 1

• (a, b, c) = (-1/3, 2, 5)
• y = (-1/3)x^2 +2x +5
• 7.90 seconds

Explanation:

From your equations in Part A, we can write the matrix equation as ...

`\left[\begin{array}{ccc}9&3&1\\25&5&1\\36&6&1\end{array}\right] \cdot\left[\begin{array}{c}a&b&c\end{array}\right] = \left[\begin{array}{c}8&(20)/(3)&5\end{array}\right]`

For the purpose of finding the inverse matrix (which we don't really need to do to solve this), it is convenient to use an augmented matrix that will give both the matrix inverse and the solution.

`\left[\begin{array}ccc9&3&1&1&0&0&8\\25&5&1&0&1&0&(20)/(3)\\36&6&1&0&0&1&5\end{array}\right]`

For the first step in the solution, we'll divide the first row by 9, then subtract 25 times that from the second row, and 36 times that from the third row. The goal of this step is to make the first column be 1, 0, 0. The result is ...

`\left[\begin{array}ccc1&(1)/(3)&(1)/(9)&(1)/(9)&0&0&(8)/(9)\\0&-(10)/(3)&-(16)/(9)&-(25)/(9)&1&0&-(140)/(9)\\0&-6&-3&-4&0&1&-27\end{array}\right]`

For the second step in the solution, we'll multiply the second row by -3/10, then subtract 1/3 times that from the first row and add 6 times that to the third row. The goal of this step is to make the second column be 0, 1, 0. The result is ...

`\left[\begin{array}c1&0&-(1)/(15)&-(1)/(6)&(1)/(10)&0&-(2)/(3)\\0&1&(8)/(15)&(5)/(6)&-(3)/(10)&0&(14)/(3)\\0&0&(1)/(5)&1&-(9)/(5)&1&1\end{array}\right]`

For the third step in the solution, we'll multiply the third row by 5, then add 1/15 of that to the first row and -8/15 of that to the second row. The goal of this step is to make the third column be 0, 0, 1. The result is ...

`\left[\begin{array}ccc1&0&0&(1)/(6)&-(1)/(2)&(1)/(3)&-(1)/(3)\\0&1&0&-(11)/(6)&(9)/(2)&-(8)/(3)&2\\0&0&1&5&-9&5&5\end{array}\right]`

The middle section of this augmented matrix is the inverse of the coefficient matrix:

`A^(-1)=\left[\begin{array}{ccc}(1)/(6)&-(1)/(2)&(1)/(3)\\-(11)/(6)&(9)/(2)&-(8)/(3)\\5&-9&5\end{array}\right]`

The right section of the augmented matrix is the solution set:

`X=\left[\begin{array}{c}a\\b\\c\end{array}\right]=\left[\begin{array}{c}-(1)/(3)\\2\\5\end{array}\right]`

__

The equation of the parabola is ...

`\boxed{y=-(1)/(3)x^2+2x+5}`

__

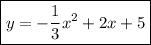
The ball will hit the ground when y=0. The values(s) of x can be found from the quadratic formula:

x = (-b±√(b²-4ac))/(2a) = (-2±√(2²-4(-1/3)(5)))/(2(-1/3))

x = (2 ± √(32/3))/(2/3) = 3±√24 = {-1.899, 7.899}

It will take about 7.90 seconds for the ball to hit the ground.