Answer:
30 seconds.
Explanation:
So, we have the equation:
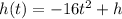
Where t is the time in seconds and h is the initial height.
A barometer falls from a weather balloon at a height of 14,400 feet. In other words, the initial height is 14,400. Substitute for h:
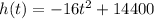
We need to find when the barometer hits the ground. Ground level is 0 feet. Therefore, we can substitute h(t) for 0 and solve for the equation (solve for t) in order to find how long (in seconds) it took for the barometer to fall:

Therefore, it took 30 seconds for the barometer to hit the ground when it fell at a height of 14,400 feet.
Edit: Spelling.