Question

Answer question 18 or 19 in the image thank you and please help

Answer 1

19)

`(1)/(2)*(1)/(4)*(1)/(8)*(1)/(16) = 2^n`

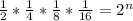
Notice that in the left side, all the numbers are powers of 2.

2 = 2^1

4 = 2^2

8 = 2^3

16 = 2^4

remember that:

(a^x)*(a^y) = a^(x+y)

then the denominator in the left is:

(2*4*8*16) = 2*(2^2)*(2^3)*(2^4) = 2^(1 + 2 + 3+ 4) = 2^8

Then we have:

`(1)/(2)*(1)/(4)*(1)/(8)*(1)/(16) = (1)/(2^8) = 2^n`

`1 = 2^8*2^n = 2^(8 + n)`

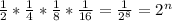
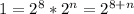
then 8 + n = 0

then n = -8.

18)

here we have:

x = (x/9) + (x/6) + (x/2) + 4 + (x/12) + 2

now in the left side we can use the common factor x and write it as:

x = x*( 1/12 + 1/9 + 1/6 + 1/2) + 6

x = x*(0.861) + 6

x - x*(0.861) = 6

x*(1 - 0.861) = 6

x = 6/(1 - 0.861) = 43.2