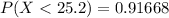Question

In the United States, the mean age of men when they marry for the first time follows the normal distribution with a mean of 24.7 years. The standard deviation of the distribution is 2.8 years. For a random sample of 60 men, what is the likelihood that the age when they were first married is less than 25.2 years

Answer 1

The likelihood is
`P(X < 25.2) = 0.91668`

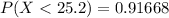
Explanation:

From the question we are told that

The population mean is
`\mu = 24.7 \ years`

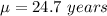
The standard deviation is
`\sigma = 2.8 \ years`

The sample size is
`n = 60 \ men`

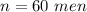
The consider random value is x = 25.2 years

Given that mean age is normally distributed, the likelihood that the age when they were first married is less than x is mathematically represented as

`P(X < x) = P( (X - \mu )/(\sigma_(\= x )) < (x - \mu )/(\sigma_(\= x )) )`

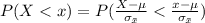
Generally
`(X - \mu )/( \sigma_(\= x)) = Z (The \ standardized \ value \ of \ X )`

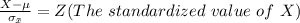
So

`P(X < x) = P(Z< (x - \mu )/(\sigma_(\= x )) )`

Where
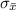`\sigma_(\= x )` is the standard error of the sample mean which mathematically evaluated as

`\sigma_(\= x ) = ( \sigma )/(√(n) )`

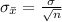
substituting values

`\sigma_(\= x ) = ( 2.8 )/(√( 60 ) )`

`\sigma_(\= x ) = 0.3615`

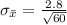
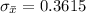
So

`P(X < 25.2) = P(Z< ( 25.2 - 24.7 )/(0.3615) )`

`P(X < 25.2) = P(Z< 1.3831 )`

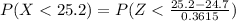
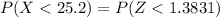
From z-table the value for P(Z< 1.3831 ) is
`P(Z < 1.3831 ) = 0.91668`

So

`P(X < 25.2) = 0.91668`