Answer:
The confidence interval is

Explanation:
From the question we are told that
The first sample size is

The second sample size is
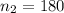
The first sample mean is
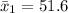
The second sample mean is
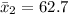
The first standard deviation is
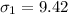
The second standard deviation is
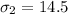
Given that the confidence level is 98% then the significance level is mathematically evaluated as
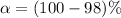
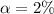
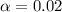
Next we obtain the critical value of
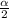 from the z-table , the value is
from the z-table , the value is
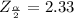
The reason we are obtaining critical value of
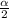
instead of
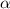
is because
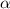
represents the area under the normal curve where the confidence level interval (

) did not cover which include both the left and right tail while
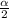
is just the area of one tail which what we required to calculate the margin of error
NOTE: We can also obtain the value using critical value calculator (math dot armstrong dot edu)
Generally the margin of error is mathematically represented as
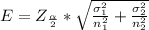
substituting values
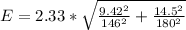
substituting values
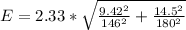
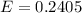
The 98% confidence interval is mathematically represented as
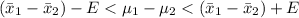
substituting values

