Answer:

Explanation:
Hello,
Let's note a and b the two numbers.
a = b - 5
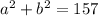
We replace a in the second equation and we solve it

It means that the sum of the two roots is 5 and the product is -66.
because
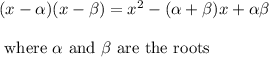
And we can notice that 66 = 6 * 11 and 11 - 6 = 5
So let's factorise it !
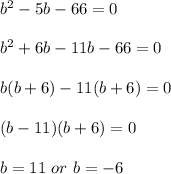
It means that the solutions are
(6,11) and (-6,-11)
I guess we are after positive numbers though.
Hope this helps.
Do not hesitate if you need further explanation.
Thank you