Question

A rectangular solid has edges whose lengths are in the ratio 1:2:3. If the volume of the solid is 864 cubic units, what are the lengths of the solid's edges?

Answer 1

Answer: 5.24 units, 10.48 units , 15.72 units

Explanation:

Volume of a rectangular solid is given by :-

V = lwh, where l = length , w= width and h = height

Given: A rectangular solid has edges whose lengths are in the ratio 1:2:3.

Let lengths of the rectangular solid x , 2 x, 3x.

volume of the solid is 864 cubic units

Then, Volume of rectangle =
`x (2x)(3x) =864\ \text{cubic units}`

`\Rightarrow\ 6x^3 = 864\\\\\Rightarrow\ x^3 =144\\\\\Rightarrow\ x=(144)^{(-1)/(3)}\approx5.24`

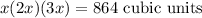
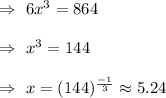
Lengths of rectangular solid 5.24 units, 2 (5.24) units , 3(5.24) units

= 5.24 units, 10.48 units , 15.72 units