Question

g There are 60 mountain climbers in a club. 10 of these have climbed Mt. Everest. 15 have climbed Mt. Rainier. 8 have climbed both. How many have not climbed either mountain?

Answer 1

43 mountain climbers have not climbed either mountain.

Explanation:

Total number of mountain climbers, i.e. n(U) = 60

Number of mountain climbers who have climbed Mt. Everest, n(E) = 10

Number of mountain climbers who have climbed Mt. Rainier, n(R) = 15

Number of mountain climbers who have climbed both, n(E
`\cap` R) = 15

Using the formula to find number of climbers who have climbed either of the mountains:

`n(A \cup B) = n(A)+n(B)-n(A\cup B )`

`\therefore n(E \cup R) = n(E)+n(R)-n(E\cup R )\\\Rightarrow n(E \cup R) = 10+15-8 = 17`

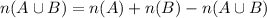
To find, who have not climbed either mountain:

`n(E\cup B)'=n(U) - n(E\cap B)\\\Rightarrow n(E\cup B)'=60 - 17 = \bold{43}`

So, the answer is:

43 mountain climbers have not climbed either mountain.