Question

Triangle ABC has vertices at A(2,5), B(4,11) and C(-1,6). Determine the angles in this triangle.

I need this solved using vectors please

Answer 1

The angles are

∠A = 90°, ∠B = 26.56°, ∠C = 63.43°

Explanation:

We have that the angles of a vector are given as follows;

`cos\left ( \theta \right ) = \frac{\mathbf{a\cdot b}}{\left | \mathbf{a} \right |\left | \mathbf{b} \right |}`

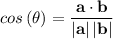
Whereby the vertices are represented as

A= (2, 5, 0), B = (4, 11, 0), C = (-1, 6, 0),

AB =(4, 11, 0) - (2, 5, 0) = (2, 6, 0) , BA = (-2, -6, 0)

BC = (-1, 6, 0) - (4, 11, 0) = (-5, -5, 0), CB = (5, 5, 0)

AC = (-1, 6, 0) - (2, 5, 0) = (-3, 1, 0), CA = (3, -1, 0)

θ₁ = AB·AC

a·c = a₁c₁ + a₂c₂ + a₃c₃ = 2×(-3) + 6×1 = 0

Therefore, θ₁ = 90°

BA·BC = (-2)×(-5) + (-6)×(-5) = 40

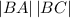`{\left | \mathbf{}BA \right |\left | \mathbf{}BC \right |}` = (√((-2)² + (-6)²)) × (√((-5)² + (-5)²)) = 44.72

cos(θ₂) = 40/44.72 = 0.894

cos⁻¹(0.894) =θ₂= 26.56°

CA·CB = 5×3 + 5×(-1) = 10

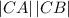`{\left | \mathbf{}CA \right |\left | \mathbf{}CB \right |}` = (√((3)² + (-1)²)) × (√((5)² + (5)²)) = 22.36

10/22.36 = 0.447

cos(θ₃) = 0.447

θ₃ = cos⁻¹(0.447) = 63.43°.