Question

A group of students estimated the length of one minute without reference to a watch or​ clock, and the times​ (seconds) are listed below. Use a 0.01 significance level to test the claim that these times are from a population with a mean equal to 60 seconds. Does it appear that students are reasonably good at estimating one​ minute?

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

Yes the students are reasonably good at estimating one​ minute

a

Option A is correct

b

The test statistics is
`t = 0.354`

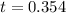
Explanation:

From the question we are told that

The set of data is

68, 82 , 38 , 62 , 41, 25 , 57 , 64, 67, 47, 61, 71, 91, 87, 64

The population mean is
`\mu = 60`

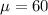
The level of significance is given as
`\alpha = 0.01`

The critical value for this level of significance obtained from the normal distribution table is

`Z_(\alpha ) = 2.33`

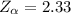
The null hypothesis is

`H_o : \mu = 60 \ seconds`

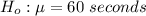
The alternative hypothesis is

`Ha : \mu \\e 60 \ seconds`

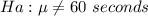
Generally the sample mean is mathematically represented as

`\= x = (\sum x_i )/(n )`

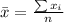
where n = 15

So

`\= x = ( 68+ 82 + 38 + 62 + 41+ 25 + 57 + 64+67+ 47+ 61+ 71+ 91+ 87+ 64)/(15)`

`\= x = 61.67`

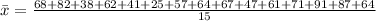
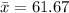
The standard deviation is mathematically represented as

`\sigma =\sqrt{ ( \sum (x_i - \= x )^2)/(n) }`

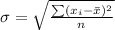
substituting values

`\sigma =\sqrt{ ( \sum (68-61.67)^2 + ( 82-61.67 )^2 + (38 -61.67)^2 + 62-61.67)^2 + (41-61.67)^2 +(25-61.67)^2 +( 57+61.67)^2 )/(15) }`
`\sqrt{ ( ( \cdot \cdot + ( 64-61.67)^2 + (67-61.67)^2 +(47-61.67)^2 + (61-61.67)^2+ (71-61.67)^2 + (91 -61.67)^2+( 87-61.67)^2 + (64-61.67)^2)/(15) }`=>
`\sigma = 18.23`

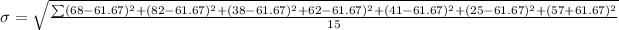
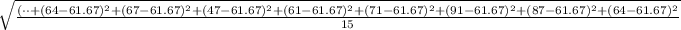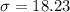
The test statistics is evaluated as

`t = (\= x - \mu )/( (\sigma )/(√(n) ) )`

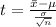
substituting values

`t = (61.67 -60 )/( (18.23 )/(√( 15) ) )`

`t = 0.354`

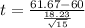
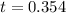
Now comparing the statistics and the critical value of the level of significance we see that the the test statistics is less than the critical value

Hence the we fail to reject the null hypothesis which mean that these times are from a population with a mean equal to 60 seconds

So we can state that yes the students are reasonably good at estimating one minute given that the sample mean is not far from the population mean