Question

Given: EG - diameter m arc FG =41°, m arc EH =53° Find: m∠E, m∠GPF

Answer 1

b

Explanation:

Answer 2

Answer: m∠E = 20.5°

m∠GPF = 47°

Step-by-step explanation: An inscribed angle is an alge formed with its vertex on the circle. Its relation with arc is that the measure of an inscribed angle is half the measure of the intersected arc. For that reason:

m∠E =
`(arcFG)/(2)`

m∠E =
`(41)/(2)`

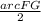
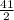
m∠E = 20.5°

Angle in F is:

m∠F =
`(arcEH)/(2)`

m∠F =
`(53)/(2)`

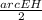
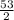
m∠F = 26.5°

The angle GPF is external to the triangle EPF, so the angle can be found by the following definition: The measure of an external angle of a triangle equals the sum of the non-adjacent angles, i.e.:

m∠GPF = m∠E + m∠F

m∠GPF = 20.5 + 26.5

m∠GPF = 47°