Question

A simple random sample from a population with a normal distribution of 102 body temperatures has x overbarequals98.40degrees Upper F and sequals0.66degrees Upper F. Construct an 80​% confidence interval estimate of the standard deviation of body temperature of all healthy humans. Is it safe to conclude that the population standard deviation is less than 1.80degrees Upper F​?

Answer 1

It is 80% statistically safe to conclude that the population standard deviation is less than 1.8°F

Explanation:

The given information are;

The sample size, n = 102

The sample mean = 98.4°F

The sample standard deviation = 0.66°F

`\sqrt{\frac{\left (n-1 \right )s^(2)}{\chi _(\alpha /2)^{}}}< \sigma < \sqrt{\frac{\left (n-1 \right )s^(2)}{\chi _(1-\alpha /2)^{}}}`

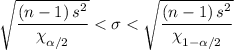
α = 0.2, ∴ α/2 = 0.1

`\chi _(1-\alpha /2)` =
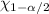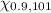`\chi _(0.9, 101)` = 83.267

`\chi _(\alpha /2)` =
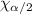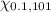`\chi _(0.1, 101)` = 119.589,

Which gives;

`\sqrt{(\left (102-1 \right )0.66^(2))/(119.589)^{}}}< \sigma < \sqrt{(\left (102-1 \right )0.66^(2))/(83.267)^{}}}`

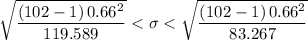
0.607 < σ <0.727

Therefore, it is 80% statistically safe to conclude that the population standard deviation is less than 1.8°F.