Answer:

Explanation:
Given
Function;
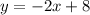
Required
Find an equation perpendicular to the given function if it passes through (-3,9)
First, we need to determine the slope of:
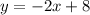
The slope intercept of an equation is in form;

Where m represent the slope
Comparing
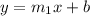 to
to
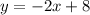 ;
;
We'll have that
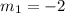
Going from there; we need to calculate the slope of the parallel line
The condition for parallel line is;
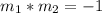
Substitute
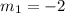
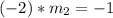
Divide both sides by -2
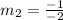
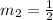
The point slope form of a line is;
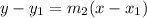
Where
 and
and
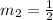
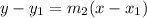 becomes
becomes
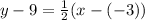
Open the inner bracket

Hence, the point slope form of the perpendicular line is:
