How many triangles does a=6 b=10 A=33° create?

Question

asked Jul 3, 2021 18.7k views

1 Answer

Igor Skoldin · Answer 1 · 2021-07-08T01:41:18+0000

Answer:

2 triangles are possible.

Explanation:

Given

a=6

b=10

$\angle$ A=33°

To find:

Number of triangles possible ?

Solution:

First of all, let us use the sine rule:

As per Sine Rule:

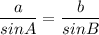
(a)/(sinA)=(b)/(sinB)

And let us find the angle B.

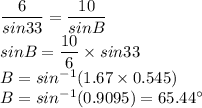
$(6)/(sin33)=(10)/(sinB)\\sinB = (10)/(6)* sin33\\B =sin^(-1)(1.67 * 0.545)\\B =sin^(-1)(0.9095) =65.44^\circ$

This value is in the 1st quadrant i.e. acute angle.

One more value for B is possible in the 2nd quadrant i.e. obtuse angle which is: 180 - 65.44 =
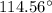
$114.56^\circ$

For the value of
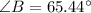$\angle B = 65.44^\circ$ , let us find
$\angle C$ :

$\angle A+\angle B+\angle C = 180^\circ\\\Rightarrow 33+65.44+\angle C = 180\\\Rightarrow \angle C = 180-98.44 = 81.56^\circ$

Let us find side c using sine rule again:

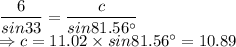
$(6)/(sin33)=(c)/(sin81.56^\circ)\\\Rightarrow c = 11.02 * sin81.56^\circ = 10.89$

So, one possible triangle is:

a = 6, b = 10, c = 10.89

$\angle$ A=33°,
$\angle$ A=65.44°,
$\angle$ C=81.56°

For the value of
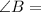
$\angle B =$
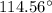$114.56^\circ$ , let us find
$\angle C$ :

$\angle A+\angle B+\angle C = 180^\circ\\\Rightarrow 33+114.56+\angle C = 180\\\Rightarrow \angle C = 180-147.56 = 32.44^\circ$

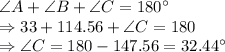
Let us find side c using sine rule again:

$(6)/(sin33)=(c)/(sin32.44^\circ)\\\Rightarrow c = 11.02 * sin32.44^\circ = 5.91$

So, second possible triangle is:

a = 6, b = 10, c = 5.91

$\angle$ A=33°,
$\angle$ A=114.56°,
$\angle$ C=32.44°

So, answer is : 2 triangles are possible.