Question

Carter is choosing clay for his pottery class. Clay is sold in three different-shaped solids at the craft store. The dimensions of each of these shapes is shown below. Find the amount of clay in each solid. Use 3.14 for Pi

After you found the amount for each solid, use them to answer this At the craft store discussed above, the clay cone is $12, the clay cylinder is $30, and the clay sphere is $28. Which is the best buy? Explain.

Answer 1

Answer: sphere

Explanation:

For cone,

Radius = 9 in.

height = 12 in.

Volume =
`(1)/(3)\pi r^2h`

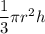
Then, Volume =
`(1)/(3)(3.14)(9)^2(12)=1017.36\ \text{cubic inches}`

For cylinder,

Radius = 9 in.

height = 12 in.

Volume =
`\pi r^2h`

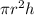
Then, volume =
`(3.14)(9)^2(12)=3052.08\text{ cubic inches}`

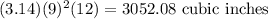
For sphere,

Radius = 9 in.

Volume =
`(4)/(3)\pi r^3`

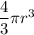
Then, volume =
`(4)/(3)(3.14)(9)^3=3052.08\text{ cubic inches}`

For best buy, we require highest volume but lowest cost.

Thus, Volume of cone < Volume of cylinder and volume of sphere.

Volume of cylinder = volume of sphere.

But the cost of the sphere < cost of cylinder as $28<$30.

So, the sphere would be the best buy as it has the greatest volume but low cost.