Answer:
The resulting graph is
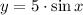 .
.
Explanation:
The resulting function is of the form:
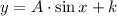
Where:
 - Independent variable, dimensionless.
- Independent variable, dimensionless.
 - Dependent variable, dimensionless.
- Dependent variable, dimensionless.
 - Amplitude, dimensionless.
- Amplitude, dimensionless.
 - Midpoint value, dimensionless.
- Midpoint value, dimensionless.
The sine function is bounded, between -1 and 1, and must be multiplied by a stretch factor. That is:
 . According to the graph, the function is bounded between 5 (
. According to the graph, the function is bounded between 5 (
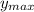 ) and -5 (
) and -5 (
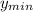 ), and the midpoint value (
), and the midpoint value (
 ) is 0. The amplitude is determined by the following calculation:
) is 0. The amplitude is determined by the following calculation:
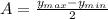
If
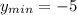 and
and
 , then:
, then:
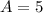
The resulting graph is
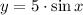 .
.