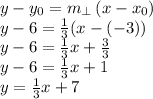Answer:

Explanation:
We need to find the equation of a line perpendicular to
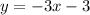 , which passes through the point (-3, 6).
, which passes through the point (-3, 6).
Recall that a line perpendicular to a line of the form:
 , must have a slope which is the opposite of the reciprocal of the slope of the original line. that is, a slope of the form;
, must have a slope which is the opposite of the reciprocal of the slope of the original line. that is, a slope of the form;
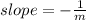
Then, in our case, since the original line has slope "-3", a perpendicular line to it should have a slope given by:
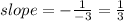
We now know the slope, and also a point for this new line, so we use the point-slope form of a line: