Question

The hypotenuse of an isosceles right triangle is 4sqrt(2) units. How many square units are in the area of the triangle?

Answer 1

19.595 units²

Explanation:

Find length of other sides:

An isosceles triangle has 2 sides equal. It has two 45 degrees angles and one 90 degrees angle. We can use Pythagorean theorem.

`(4√(2) )^2 =a^2 +a^2`

`32 =2a^2`

`16=a^2`

`4=a`

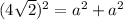
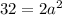
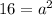
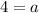
The 2 equal sides measure 4 units.

Find area:

base × height × 1/2

The height can be found by Pythagorean theorem.

height² = 4² + 4sqrt(2)²

height² = 16 + 32

height² = 48

height = 6.928

base is given

4sqrt(2) × 6.928 × 1/2

= 19.595343

Answer 2

8sqrt(2)

Explanation:

An isosceles is a triangle with 2 45 degree angles and one 90 degree angle.

if the hypotenuse side=4sqrt(2) than that means the other 2 sides have to be just 4 units.

the formula for a triangle is than (base×height)÷2

4×4sqrt(2)=16sqrt(2)

(16sqrt(2))/2=8sqrt(2)