Answer:
m∠DEA = 62°
m∠ADB (arc) = 194°
Angle ∠ADB = 21°.
Explanation:
The given information are;
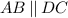, m CB (arc) = 62°, m∠DAB (arc) = 104°
arc∠BCD = 360° - 104° = 256°
m DC (arc) = arc∠BCD - arc CB = 256° - 62° (Sum of angles)
Therefore DC (arc) = 194°
m DA ≅ m CB = 62° (Parallel lines congruent arc theorem. Arc between two parallel lines)
m∠DEA = 1/2×(arc DA + arc CB) = 1/2×(62° + 62°) =62°
m∠DEA = 62°
Arc AB = m∠DAB (arc) - m DA = 104° - 62° = 42°
m∠ADB (arc) = 360 - m∠DAB (arc) - m CB (arc) (Sum of angles around a circle or point)
∴ m∠ADB (arc) = 360 - 104 - 62 = 194°
m∠ADB (arc) = 194°
Angle ADB = subtended by arc AB = ∴1/2×arc AB
Angle ∠ADB = 42/2 = 21°.
Angle = 21°