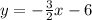Question

What is the equation of the line that passes through (–2, –3) and is perpendicular to 2x – 3y = 6?

Answer 1

Answer: A.

explanation:just did the test

Answer 2

`y=-(3)/(2)x-6`

Explanation:

Since the line needs to be perpendicular to
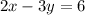`2x-3y=6`, that means the slope of the line must be the opposite reciprocal. Rearrange the equation
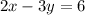`2x-3y=6` to solve for the value of y, with variable y on the left side.

`-3y=-2x+6\\y=(2)/(3) x-2`

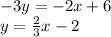
So, the slope of the line given already is
`(2)/(3)`. The opposite reciprocal of this is
`-(3)/(2)`.

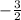From what information we know so far (the slope) about the equation of the line we are trying to find, we can write a basic equation that allows us to solve for the y-intercept. Use the equation
`y=mx+b`, where m is the slope (which we already found) and b is the y-intercept.

`y=-(3)/(2)x+b`

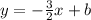
Since we are given a set of coordinate points that the line must pass through, we can substitute (-2, -3) in for x and y in the equation above. Then, solve for the value of b, which is our y-intercept.

`-3=-(3)/(2)(-2)+b\\ -3=3+b\\b=-6`

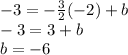
Now we have all the necessary information to create our equation.

`y=-(3)/(2)x-6`