Answer:
Option c.
Explanation:
From the given table, it is clear that
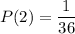

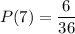
The increasing rate of probability between a sum of 2 and a sum of 6 is
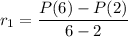
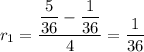
The increasing rate of probability between a sum of 6 and a sum of 7 is

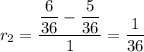
Since
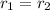 , therefore the probability increases at the same rate over both intervals.
, therefore the probability increases at the same rate over both intervals.
Hence, the correct option is c.