Question

What is the value of the 35th term in the sequence -15, -11, -7, ...? 121 125 151 374

Answer 1

121 and 257

Explanation:

So we would have our equation for arithmetic sequences which is
`a_(n) =a_(1) +(n-1)d` a1 is the first term, n is the term we want to know, and d is the common difference. We would plug in the numbers into the equation so we would get
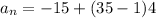`a_(n) =-15+(35-1)4`. And if you simplify you would get
`a_(n) =121`.

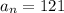Than for the other one we would do the same thing so you would get
`a_(n) = 121+(35-1)4` and if you simplify you would get
`a_(n) =257`.

Answer 2

121

Explanation:

This is an arithmetic sequence.

First term a = -15

Common difference [d] = second term - first term

= -11 - [-15] = -11 + 15 = 4

nth term = a + (n-1) * d

35th term = -15 + (35 - 1) * 4

= -15 + 34 * 4

= - 15 + 136

= 121