Answer:
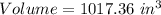 -- Cone
-- Cone
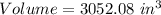 -- Cylinder
-- Cylinder
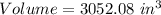 -- Sphere
-- Sphere
Best Buy: Sphere Clay
Explanation:
Given
Solid Shapes: Cone, Cylinder, Sphere
Cost of Cone Clay = $12
Cost of Cylinder Clay = $30
Cost of Sphere Clay = $28
Required
Determine the volume of each shape
Which is the best buy
CONE
Calculating Volume
The volume of a cone is calculated as thus;
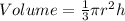
From the attached diagram
Radius, r = 9 inches; Height, h = 12 inches and
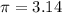
Substitute these values in the above formula;

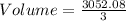
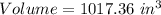
Calculating Volume:Price Ratio
The unit cost of the cone is calculated as thus;

Where
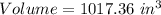
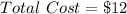 (Given)
(Given)
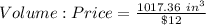
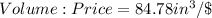
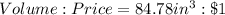
CYLINDER
Calculating Volume
The volume of a cylinder is calculated as thus;

From the attached diagram
Radius, r = 9 inches; Height, h = 12 inches and
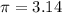
Substitute these values in the above formula;
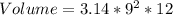
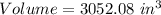
Calculating Volume:Price Ratio
The unit cost of the cone is calculated as thus;

Where
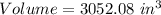
 (Given)
(Given)
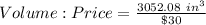
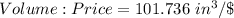
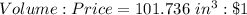
SPHERE
Calculating Volume
The volume of a sphereis calculated as thus;
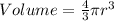
From the attached diagram
Radius, r = 9 inches; and
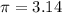
Substitute these values in the above formula;
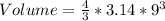
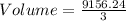
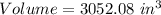
Calculating Volume-Price ratio
The unit cost of the cone is calculated as thus;

Where
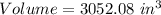
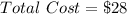 (Given)
(Given)
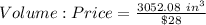
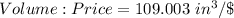
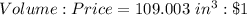
Comparing the Volume:Price ratio of the three clay;
The best buy is the sphere because it has the highest volume:price ratio.
Having the highest volume:price ratio means that with $1, one can get more clay from the sphere compared to other types of clay