Answer:
The probability that Pat will pass the exam is 0.02775.
Explanation:
We are given that exam consists of 100 true-false questions. Pat plans to guess the answer to each question without reading it.
If a grade on the exam is 60% or more, Pat will pass the exam.
Let X = grade on the exam by Pat
The above situation can be represented through binomial distribution such that X ~ Binom(n = 100, p = 0.50).
Here the probability of success is 50% because there is a true-false question and there is a 50-50 chance of both being the correct answer.
Now, here to calculate the probability we will use normal approximation because the sample size if very large(i.e. greater than 30).
So, the new mean of X,
 =
=
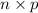 =
=
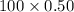 = 50
= 50
and the new standard deviation of X,
 =
=
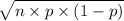
=
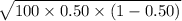
= 5
So, X ~ Normal(
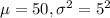 )
)
Now, the probability that Pat will pass the exam is given by = P(X
 60)
60)
P(X
 60) = P(
60) = P(


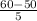 ) = P(Z
) = P(Z
 2) = 1 - P(Z < 2)
2) = 1 - P(Z < 2)
= 1 - 0.97725 = 0.02275
Hence, the probability that Pat will pass the exam is 0.02775.