Question

9. You are given a number of 10 Ω resistors, each capable of dissipating only 1.0 W without being destroyed. What is the minimum number of such resistors that you need to combine in series or in parallel to make a 10 Ω resistance that is capable of dissipating at least 5.0 W?

Answer 1

To achieve a 10 Ω resistance capable of dissipating at least 5.0 W, we need either 5 resistors in series or 5 resistors in parallel.

Step-by-step explanation:

To make a 10 Ω resistance capable of dissipating at least 5.0 W, we need to combine resistors in either series or parallel.

In series, the minimum number of resistors needed can be found by dividing the power dissipation requirement by the power dissipated by each resistor. In this case, 5.0 W / 1.0 W = 5 resistors.

In parallel, the total power dissipated is the sum of the power dissipated by each resistor. To achieve at least 5.0 W, we need a total power dissipation of 5.0 W. Since each resistor is capable of dissipating 1.0 W, we would need 5 resistors in parallel.

Answer 2

here are 9 resistors, forming a group of 3 resistors in parallel and each group in series with the other.

Step-by-step explanation:

Let's work carefully this exercise, they indicate that the total resistance 10 ohm and dissipates 5W, so we can use the power equation to find the circuit current

P = Vi = i² R

i = √ P / R

i = √ (5/10)

i = 0.707 A

This is the current that must circulate in the circuit.

Let's build a circuit with three resistors in series and each resistor in series has three resistors in parallel

The equivalent resistance is

1 /
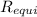`R_(equi)` = 1/10 + 1/10 + 1/10 = 3/10

Requi = 10/3

Requi = 3.3 Ω

The current in the three series resistors is I = 0.707 A, and this is divided into three equal parts for the parallel resistors

current in each residence in parallel

i_P = 0.707 / 3

I_p = 0.2357 A

now let's look at the power dissipated in each resistor

P = R i²

P = 10 0.2357²

P = 0.56 W

the power dissipated by each resistance is within the range of 1 A, let's see the total power that the 9 resistors dissipate

P_total = 9 P

P = total = 9 0.56

P_total = 5 W

we see that this combination meets the specifications of the problem.

Therefore there are 9 resistors, forming a group of 3 resistors in parallel and each group in series with the other.