Question

Write the equation of the conic section satisfying the given conditions. focus at the pole, e = 3/4, horizontal directrix 2 units above the pole

Answer 1

The equation in the polar form is;

`r = (6)/(4 + 3 \cdot sin(\theta))`

Explanation:

e = 3/4 > 1, we have an hyperbola

The polar equation of a conic is of the form;

For vertical directrix

`r = (k \cdot e)/(1\pm e \cdot cos (\theta))`

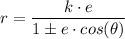
For horizontal directrix

`r = (k \cdot e)/(1\pm e \cdot sin(\theta))`

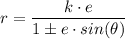
Where;

k = Distance from the focus to the directrix = 2

We have;

`r = (2 \cdot (3)/(4) )/(1 + (3)/(4) \cdot sin(\theta))`

`r = ((3)/(2) )/(1 + (3)/(4) \cdot sin(\theta))`

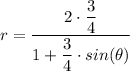
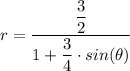
Which gives the equation in the polar form as follows;

`r = (6)/(4 + 3 \cdot sin(\theta))`.