Question

I need some help with a long chemistry problem. Anything is appreciated!

You arrive at a crime scene and are told the body of the victim is in the 10 m deep pool. You walk over to what you are told is a 12 m in diameter, cylindrical pool. From the outside of the pool, you can see that the body looks badly burnt. Your partner says, “It looks like our victim had been burned alive and tried to put out the fire by jumping in the pool. The victim likely drowned to death.”


Something does not sit right with you though. If there was a fire, where did it start? There are no signs of combustion anywhere. You aren’t so sure and ask the crime scene investigator to run a sample of the pool water before letting anybody try to pull the body out.


The CSI comes back to you and tells you that normal pool water pH is roughly around 7.2, but the pool pH is actually highly basic at a level of 13 with a concentration of hydroxide ions at 1.0 x 10-1 mol/L. It becomes obvious to you that the body wasn’t burned before going in to the pool , but AFTER and there was no fire needed!


You order the body to be removed from the pool, but the CSI interjects, “It would be too dangerous with a pH that high. I suggest you get some vinegar from the store and pour it in to the pool before hand to drop the pH to 7. Draining the pool would take far too long and we need to examine the body as soon as possible.” She asks one of your constables to go to the store to purchase 5 – 4L jugs of vinegar (pH = 2) to pour in the pool, as she states it is enough to bring the pH to a safe level of 7.


It sounds like it could be enough vinegar based on your knowledge of acids and bases, but you want to double-check her estimate before sending your constable to the store. Verify whether or not she is correct using calculations. A diagram may help you with your calculations

Answer 1

The CSI is wrong.

Step-by-step explanation:

1. Find the volume of the pool

The formula for the volume of a cylinder is V = πr²h .

D = 12 m; h = 10 m

r = D/2 = (12 m/2) = 6.0 m

V = πr²h = π × (6.0 m)² × 10 m = π × 36 m²× 10 m = 360π m³ = 1100 m³

= 1.1. × 10⁶ L

2. Calculate the moles of OH⁻

n = cV = 1.0 × 10⁻² mol·L⁻¹ × 1.3 × 10⁶ L = 11 000 mol of OH⁻

3. Calculate the moles of acetic acid needed for neutralization

HA + OH⁻ ⟶ A⁻ + H₂O

The molar ratio of is 1 mol HA:1 mol OH⁻, so you need 11 000 moL of acetic acid.

4. Calculate the actual moles of acetic acid

You have four 5 L jugs of acetic acid pH 2 .

Volume = 20 L

[H⁺] = 10⁻² mol·L⁻¹ = 0.01 mol·L⁻¹

(a) Set up an ICE table

HA + H₂O ⇌ A⁻ + H₃O⁺

I/mol·L⁻¹: c 0 0

I/mol·L⁻¹: - 0.01 +0.01 +0.01

I/mol·L⁻¹: c - 0.01 0.01 0.01

`K_{\text{a}} = \frac{\text{[A]}^(-)\text{[H$_(3)$O$^(+)$]}}{\text{[HA]}} = 1.76 * 10^(-5)`

(b) Calculate the concentration of acetic acid

`\begin{array}{rcl}\frac{\text{[A]}^(-)\text{[H$_(3)$O$^(+)$]}}{\text{[HA]}}& = & 1.76 * 10^(-5)\\\\(0.01* 0.01)/(c)& = & 1.76 * 10^(-5)\\\\1 * 10^(-4) & = & 1.76 * 10^(-5)c\\c & = & (1 * 10^(-4))/(1.76 * 10^(-5))\\\\ & = & \text{6 mol/L}\\\end{array}`

The concentration of the acetic acid is 6 mol·L⁻¹

(c) Calculate the moles of acetic acid

`n = \text{20 L} * \frac{\text{6 mol}}{\text{1 L}} = \textbf{100 mol}`

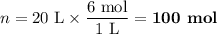
You have 100 mol of acetic acid.

The CSI is wrong.

You don't have enough acetic acid to neutralize the pool.