Question

The volume of a rectangular prism is (x4 + 4x3 + 3x2 + 8x + 4), and the area of its base is (x3 + 3x2 + 8). If the volume of a rectangular prism is the product of its base area and height, what is the height of the prism? PLEASE COMMENT, I Can't SEE ANSWERS CAUSE OF A GLITCH

Answer 1

`x +1 - (4)/(x^3 + 3x^2 + 8)`

Explanation:

`volume=base \: area * height`

`height=(volume)/(base \: area)`

`\mathrm{Solve \: by \: long \: division.}`

`h=((x^4 + 4x^3 + 3x^2 + 8x + 4))/((x^3 + 3x^2 + 8))`

`h=x + (x^3 + 3x^2 + 4)/(x^3 + 3x^2 + 8)`

`h=x +1 - (4)/(x^3 + 3x^2 + 8)`

Answer 2

x + 1 - ( 4 / x³ + 3x² + 8 )

Explanation:

If the volume of this rectangular prism ⇒ ( x⁴ + 4x³ + 3x² + 8x + 4 ), and the base area ⇒ ( x³ + 3x² + 8 ), we can determine the height through division of each. The general volume formula is the base area
`*` the height, but some figures have exceptions as they are " portions " of others. In this case the formula is the base area
`*` height, and hence we can solve for the height by dividing the volume by the base area.

Height = ( x⁴ + 4x³ + 3x² + 8x + 4 ) / ( x³ + 3x² + 8 ) =
`(x^4+4x^3+3x^2+8x+4)/(x^3+3x^2+8)` =
`x+(x^3+3x^2+4)/(x^3+3x^2+8)` =
`x+1+(-4)/(x^3+3x^2+8)` =
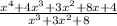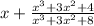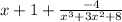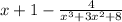`x+1-(4)/(x^3+3x^2+8)` - and this is our solution.