Answer:
The rhombus ABCD has an area of 22 square units.
Explanation:
The coordinates of rhombus ABCD are shown in the image attached below. The area of the rhombus can be found in terms of their diagonals, which are now calculated by Pythagorean Theorem:
![AC = \sqrt{[6-(-4)]^(2)+[8-(-4)]^(2)}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/8gd9cbtzbj0x1dhi77i0y7brj2afqon209.png)
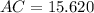
![BD = \sqrt{(4-6)^(2)+[0-(-2)]^(2)}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/ro85fny993x95p7a898hvx1fteckz2w0j0.png)
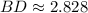
The area of the rhombus is: (
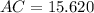 and
and
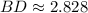 )
)
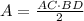
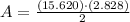
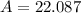
The rhombus ABCD has an area of 22 square units.