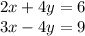Question

Which system of equations has only one solution? 4 x + 2 y = 8. Negative 4 x minus 2 y = 3. Negative 5 x + y = 6. 5 x minus y = negative 6. Negative 3 x + 4 y = 2. 3 x minus 4 y = 0. 2 x + 4 y = 6. 3 x minus 4 y = 9.

Answer 1

4

Explanation:

Answer 2

Following system of equations have exactly one solution:

`2 x + 4 y = 6\\ 3 x - 4 y = 9`

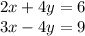
Explanation:

Given 4 system of equations:

1st

`4 x + 2 y = 8\\ -4 x -2 y = 3`

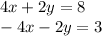
2nd

`-5 x + y = 6\\ 5 x - y = - 6`

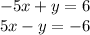
3rd

`- 3 x + 4 y = 2\\ 3 x - 4 y = 0`

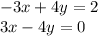
4th

`2 x + 4 y = 6\\ 3 x - 4 y = 9`

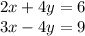
To find: Which system of equations has only one solution?

Solution:

First of all, let us learn the concept.

Let the equation of lines be:

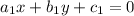`a_1x+b_1y+ c_1=0` and
`a_2x+b_2y+ c_2=0`

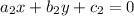
1. No solution:

There exists no solution if:

`(a_1)/(a_2)=(b_1)/(b_2)\\eq(c_1)/(c_2)`

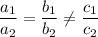
2. Infinite solutions:

There exist infinitely many solutions if:

`(a_1)/(a_2)=(b_1)/(b_2)=(c_1)/(c_2)`

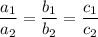
3. One solution:

There exists one solution if:

`(a_1)/(a_2)\\eq(b_1)/(b_2)`

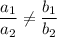
Now, let us consider the given equations one by one.

1st system of equations:

The ratio is:

`(4)/(-4) , (2)/(-2) , (8)/(3)\\-1 =-1\\eq (8)/(3)`

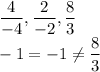
So, no solution.

2nd system of equations:

The ratio:

`(-5)/(5) , (-1)/(1) , (6)/(-6)\\-1 =-1=-1`

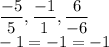
So, infinitely many solutions.

3rd system of equations:

`(3)/(-3) , (-4)/(4) , (0)/(2)\\-1 =-1\\e0`

So, no solution.

4th system of equations:

`(2)/(3) , (4)/(-4) , (6)/(9)\\(2)/(3) \\e-1`

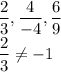
Hence, only one solution.

So, the answer is:

Following system of equations have only one solution:

`2 x + 4 y = 6\\ 3 x - 4 y = 9`