Answer:
f(n) = 1.9+0.6n
Explanation:
Given the sequence that represents the diameter of a circle
2.5 cm, 3.1 cm, 3.7 cm and 4.3 cm. This sequence forms an arithmetic progression with a common difference.
nth term of an arithmetic progression is expressed as
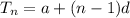
a is the first term of the sequence
n is the number of terms
d is the common difference.
From the sequence above, the first term a = 2.5
common difference = 3.1-2.5 = 3.7-3.1 = 4.3-3.7 = 0.6
Substituting this given values into the formula above will give;
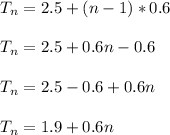
If f(n) represent diameter in centimetres and n the term number in the sequence, the equation that represents the sequence of diameters is
f(n) = 1.9+0.6n