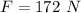Answer:
The force is
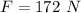
Step-by-step explanation:
From the question we are told that
The mass of the block is
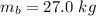
The coefficient of static friction is
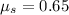
The coefficient of kinetic friction is

The normal force acting on the block is
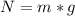
substituting values
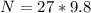
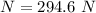
Given that the force we are to find is the force required to get the block to start moving then the force acting against this force is the static frictional force which is mathematically evaluated as
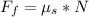
substituting values
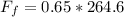
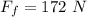
Now for this block to move the force require is equal to
 i.e
i.e
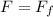
=>