Answer:
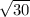
Explanation:
Given,
Perpendicular ( p ) = 3√2
Base ( b ) = 2√3
Hypotenuse ( h ) = ?
Now, let's find the length of the hypotenuse:
Using Pythagoras theorem:
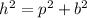
plug the values
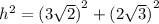
To raise a product to a power, raise each factor to that power
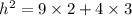
Multiply the numbers
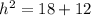
Add the numbers
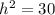
Take the square root of both sides of the equation
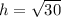
Hope this helps...
Best regards!!