Question

Find the minimum sample size necessary to be 99% confident that the population mean is within 3 units of the sample mean given that the population standard deviation is 29. (a) What is the critical value that corresponds to the given level of confidence? Round your answer to two decimals, and remember that critical values are always positive.

Answer 1

623

Explanation:

Given that margin of error (E) = 3 unit, standard deviation (σ) = 29, sample size (n) = ?

a) The confidence (C) = 99% = 0.99

α = 1 - C = 1 - 0.99 = 0.01

α/2 = 0.01 / 2 = 0.005

From the normal distribution table, The z score of α/2 (0.005) is the critical value and it corresponds to the z score 0.495 (0.5 - 0.005) which is 2.58.

`critical\ value = z_{(\alpha)/(2) }=z_(0.005)=2.58\\`

b) The margin of error (E) is given as:

`E=z_{(\alpha)/(2) }*(\sigma)/(√(n) )\\\\√(n)= z_{(\alpha)/(2) }*(\sigma)/(E )\\ \\n=( z_{(\alpha)/(2) }*(\sigma)/(E ))^2\\\\Substituting:\\\\n=(2.58*(29)/(3) )^2=622.0036\\\\\\n=623(to\ the \ next\ whole\ number)`

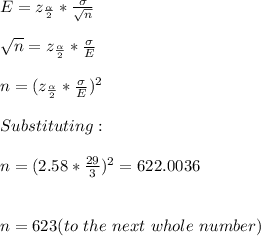
The minimum sample size (n) is 623