Question

There are 45 balloons: 15 are blue; 20 are green; 10 are red. 3 balloons are selected for the float. Leaving your answers in combinatorics format, how many ways can all 3 be selected such that they are the same color.

Answer 1

Answer: Required number of ways = 1715

Explanation:

Given, there are 45 balloons: 15 are blue; 20 are green; 10 are red.

3 balloons are selected for the float.

Number of combinations to select r things out of n things :
`^nC_r=(n!)/(r!(n-r)!)`

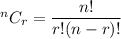
So, the number of ways to select 3 ballons such that they are the same color = (Ways to select all blue ) x (Ways to select all green ) x (Ways to select all red)

`^(15)C_3+^(20)C_3+^(10)C_3\\\\=(15!)/(12!*3!)+(20!)/(17!*3!)+(10!)/(7!*3!)\\\\=(15*14*13)/(6)+(20*19*18)/(6)+(10*9*8)/(6)\\\\=455+1140+120\\\\=1715`

Hence, Required number of ways = 1715