Answer:
Null hypothesis :
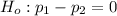
Alternative hypothesis:
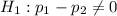
Decision Rule:
To reject the null hypothesis if z < -1.65 and z > 1.65
Conclusion:
Failed to reject null hypothesis if z > -1.65 or z < 1.65
z -value = 0.33022
P-value = 0.7414
Decision Rule:
Since the P-value is higher than the level of significance , therefore do not reject the null hypothesis at the level of significance of 0.1
Conclusion: we failed to reject null hypothesis, Therefore, the data does not believe that the true percentage of those in the first group who suffer a second episode is different from the true percentage of those in the second group who suffer a second episode
Explanation:
From the summary of the given statistical data sets.
Let consider to
 represent percentage of the first group ; &
represent percentage of the first group ; &
 represent percentage of the second group
represent percentage of the second group
The null and the alternative hypothesis can be stated s follows:
Null hypothesis :
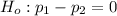
Alternative hypothesis:
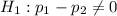
At the level of significance ∝ = 0.1; the two tailed critical value from the z-table
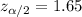
Decision Rule:
To reject the null hypothesis if z < -1.65 and z > 1.65
Conclusion:
Failed to reject null hypothesis if z > -1.65 or z < 1.65
However; from the question:
There are 55 people in the first group and this group will be administered the new drug.
There are 45 people in the second group and this group will be administered a placebo.
After one year, 11% of the first group has a second episode and 9% of the second group has a second episode.
The test statistic for the for the first group who suffered from the second episode can be denoted as :
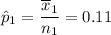
The test statistic for the for the second group who suffered from the second episode can be denoted as :
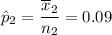
where;
 = sample size of group 1 = 55
= sample size of group 1 = 55
 = sample size of group 2 = 45
= sample size of group 2 = 45
The total probability of both group is :
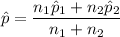
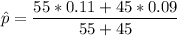
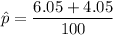
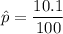
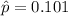
The standard error of the statistic
 an be computed as follows:
an be computed as follows:

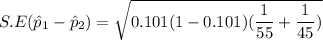
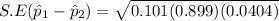
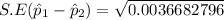

Now; The test statistics is determined to be :
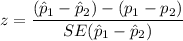
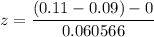
z = 0.33022
Hence; the value for the test statistics = 0.33022
the value for the test statistics = 0.33
From the z value; The P-value for the test statistics can be computed as:
P-value = 2P(Z ≥ |z|)
P-value = 2P(Z ≥ 0.33022)
P-value = 2 × P (Z ≤ - 0.33022)
From the z table Z ≤ - 0.33022 = 0.3707
P-value = 2 × 0.3707
P-value = 0.7414
Decision Rule:
Since the P-value is higher than the level of significance , therefore do not reject the null hypothesis at the level of significance of 0.1
Conclusion: we failed to reject null hypothesis, Therefore, the data does not believe that the true percentage of those in the first group who suffer a second episode is different from the true percentage of those in the second group who suffer a second episode