Answer:
(a) 4.334 × 10¹¹ joules are required to propel the rocket an unlimited distance away from Earth's surface, (b) The rocket has travelled 3999.865 miles from the Earth's surface with the half of the total work.
Step-by-step explanation:
The complete statement is: "Use the weight of the rocket to answer the question. (Use 4000 miles as the radius of Earth and do not consider the effect of air resistance.) 7 metric ton rocket (a) How much work is required to propel the rocket an unlimited distance away from Earth's surface, (b) How far has the rocket traveled when half the total work has occurred?"
(a) The work required to propel the rocket is given by the change in gravitational potential energy, whose expression derives is described below:
![U_(g, f) - U_(g, o) = -G\cdot M\cdot m \cdot \left[(1)/(r_(f))-(1)/(r_(o)) \right]](https://img.qammunity.org/2021/formulas/physics/college/4jmv9f8k0xsayr7gvrwttyg4fjnqies95b.png)
Where:
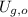 ,
,
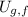 - Initial and final gravitational potential energies, measured in joules.
- Initial and final gravitational potential energies, measured in joules.
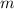 ,
,
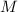 - Masses of the rocket and planet Earth, measured in kilograms.
- Masses of the rocket and planet Earth, measured in kilograms.
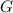 - Universal gravitation constant, measured in newton-square meters per square kilogram.
- Universal gravitation constant, measured in newton-square meters per square kilogram.
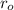 ,
,
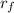 - Initial and final distances of the rocket with respect to the center of the Earth, measured in meters.
- Initial and final distances of the rocket with respect to the center of the Earth, measured in meters.
The initial distance and rocket mass are converted to meters and kilograms, respectively:
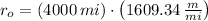
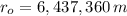
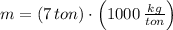
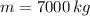
Given that
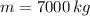 ,
,
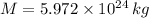 ,
,
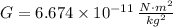 ,
,
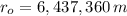 and
and
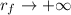 , the work equation is reduced to this form:
, the work equation is reduced to this form:
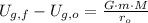
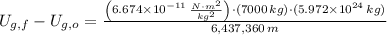
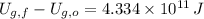
4.334 × 10¹¹ joules are required to propel the rocket an unlimited distance away from Earth's surface.
(b) The needed change in gravitational potential energy is:
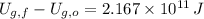
The expression for the change in gravitational potential energy is now modified by clearing the final distance with respect to the center of Earth:
![U_(g, f) - U_(g, o) = -G\cdot M\cdot m \cdot \left[(1)/(r_(f))-(1)/(r_(o)) \right]](https://img.qammunity.org/2021/formulas/physics/college/4jmv9f8k0xsayr7gvrwttyg4fjnqies95b.png)
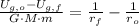
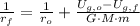
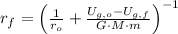
If
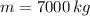 ,
,
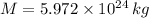 ,
,
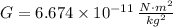 ,
,
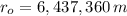 and
and
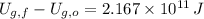 , then:
, then:
![r_(f) = \left[(1)/(6,437,360\,m)-(2.167* 10^(11)\,J)/(\left(6.674* 10^(-11)\,(N\cdot m^(2))/(kg^(2)) \right)\cdot (7000\,kg)\cdot (5.972* 10^(24)\,kg)) \right]^(-1)](https://img.qammunity.org/2021/formulas/physics/college/k8epgbzgdypaijrbkrt8u5kkv6c59skm64.png)
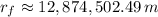
The final distance with respect to the center of the Earth in miles is:
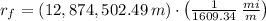
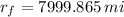
The distance travelled by the rocket is: (
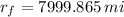 ,
,
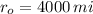 )
)
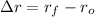
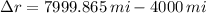
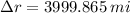
The rocket has travelled 3999.865 miles from the Earth's surface with the half of the total work.