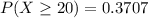Answer:
The probability is
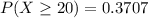
Explanation:
From the the question we are told that
The population proportion is p = 0.60
The sample size is n = 31
The mean is evaluated as
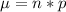
substituting values
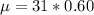
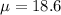
The standard deviation is evaluated as
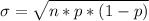
substituting values
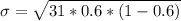
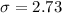
The the probability that at least 20 of them have looked at their score in the past six months is mathematically represented as
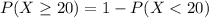
applying normal approximation we have that
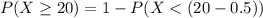
Standardizing
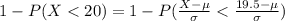
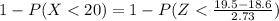
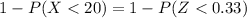
Form the standardized normal distribution table we have that
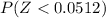 = 0.6293
= 0.6293
=>
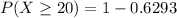
=>