Question

A compound decomposes with a half-life of 8.0 s and the half-life is independent of the concentration. How long does it take for the concentration to decrease to one-ninth of its initial value

Answer 1

The concentration takes 25.360 seconds to decrease to one-ninth of its initial value.

Step-by-step explanation:

The decomposition of the compound has an exponential behavior and process can be represented by this linear first-order differential equation:

`(dc)/(dt) = -(1)/(\tau)\cdot c(t)`

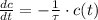
Where:

`\tau` - Time constant, measured in seconds.

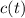`c(t)` - Concentration of the compound as a function of time.

The solution of the differential equation is:

`c(t) = c_(o) \cdot e^{-(t)/(\tau) }`

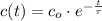
Where
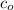`c_(o)` is the initial concentration of the compound.

The time is now cleared in the result obtained previously:

`\ln (c(t))/(c_(o)) = -(t)/(\tau)`

`t = -\tau \cdot \ln (c(t))/(c_(o))`

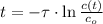
Time constant as a function of half-life is:

`\tau = (t_(1/2))/(\ln 2)`

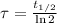
Where
`t_(1/2)` is the half-life of the composite decomposition, measured in seconds.

If
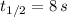`t_(1/2) = 8\,s`, then:

`\tau = (8\,s)/(\ln 2)`

`\tau \approx 11.542\,s`

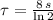
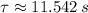
And lastly, given that
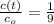`(c(t))/(c_(o)) = (1)/(9)` and
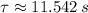`\tau \approx 11.542\,s`, the time taken for the concentration to decrease to one-ninth of its initial value is:

`t = -(11.542\,s)\cdot \ln(1)/(9)`

`t \approx 25.360\,s`

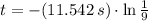
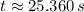
The concentration takes 25.360 seconds to decrease to one-ninth of its initial value.