Question

A clinical trial was conducted to test the effectiveness of a drug for treating insomnia in older subjects. Before​ treatment, 17 subjects had a mean wake time of 104.0 min. After​ treatment, the 17 subjects had a mean wake time of 97.5 min and a standard deviation of 21.9 min. Assume that the 17 sample values appear to be from a normally distributed population and construct a 95​% confidence interval estimate of the mean wake time for a population with drug treatments. What does the result suggest about the mean wake time of 104.0 min before the​ treatment? Does the drug appear to be​ effective?

Answer 1

The 95% confidence interval of mean wake time for a population with treatment is between 86.2401 and 108.7599 minutes.

This interval contains the mean wake time before treatment and which does not prove to be effective

Explanation:

GIven that :

sample size n = 17

sample mean
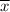`\overline x` = 97.5

standard deviation
`\sigma` = 21.9

At 95% Confidence interval

the level of significance ∝ = 1 - 0.95

the level of significance ∝ = 0.05

`t_(\alpha/2) = 0.025`

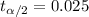
Degree of freedom df = n - 1

Degree of freedom df = 17 - 1

Degree of freedom df = 16

At ∝ = 0.05 and df = 16 , the two tailed critical value from the t-table
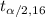`t_(\alpha/2 , 16)` is :2.1199

Therefore; at 95% confidence interval; the mean wake time is:

=
`\overline x \pm t_(\alpha/2,df) (s)/(√(n))`

=
`97.5 \pm 2.1199 * (21.9)/(√(17))`

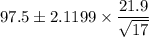
= 97.5 ± 11.2599

= (86.2401 , 108.7599)

Therefore; the mean wake time before the treatment was 104.0 min

The 95% confidence interval of mean wake time for a population with treatment is between 86.2401 and 108.7599 minutes.

This interval contains the mean wake time before treatment and which does not prove to be effective