Answer:
-1.031 m/s or
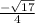
Explanation:
We take the length of the rope from the dock to the bow of the boat as y.
We take x be the horizontal distance from the dock to the boat.
We know that the rate of change of the rope length is
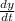 = -1 m/s
= -1 m/s
We need to find the rate of change of the horizontal distance from the dock to the boat =
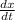 = ?
= ?
for x = 4
Applying Pythagorean Theorem we have
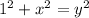 .... equ 1
.... equ 1
solving, where x = 4, we have
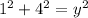
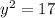
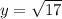
Differentiating equ 1 implicitly with respect to t, we have
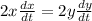
substituting values of
x = 4
y =
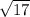
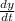 = -1
= -1
into the equation, we get
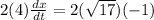
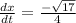 = -1.031 m/s
= -1.031 m/s