Question

Determine the values of \theta if sec\;\theta=-\frac{2}{\sqrt{3}}.

Answer 1

See below.

Explanation:

So, we have:

`\sec(\theta)=-2/√(3)`

Recall that secant is simply the reciprocal of cosine. So we can:

`\cos(\theta)=(\sec(\theta))^(-1)=(-2/√(3))^(-1)\\\cos(\theta)=-√(3)/2`

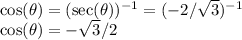
Now, recall the unit circle. Since cosine is negative, it must be in Quadrants II and/or III. The numerator is the square root of 3. The denominator is 2. The whole thing is negative. Therefore, this means that 150 or 5π/6 is a candidate. Therefore, due to reference angles, 180+30=210 or 7π/6 is also a candidate.

Therefore, the possible values for theta is

5π/6 +2nπ

and

7π/6 + 2nπ